Function-Space-Based Solution Scheme for the Size-Modified Poisson-Boltzmann Equation in Full-Potential DFT

Abstract

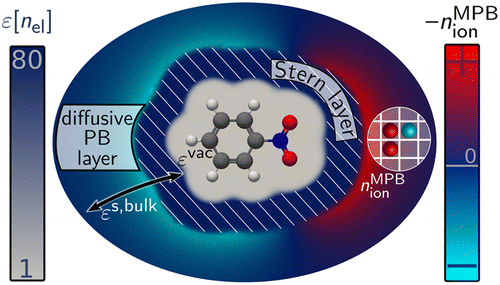
The size-modified Poisson-Boltzmann (MPB) equation is an efficient implicit solvation model which also captures electrolytic solvent effects. It combines an account of the dielectric solvent response with a mean-field description of solvated finite-sized ions. We present a general solution scheme for the MPB equation based on a fast function-space-oriented Newton method and a Green’s function preconditioned iterative linear solver. In contrast to popular multigrid solvers, this approach allows us to fully exploit specialized integration grids and optimized integration schemes. We describe a corresponding numerically efficient implementation for the full-potential density-functional theory (DFT) code FHI-aims. We show that together with an additional Stern layer correction the DFT+MPB approach can describe the mean activity coefficient of a KCl aqueous solution over a wide range of concentrations. The high sensitivity of the calculated activity coefficient on the employed ionic parameters thereby suggests to use extensively tabulated experimental activity coefficients of salt solutions for a systematic parametrization protocol.